
Reproduced with permission from Physics Today, 27(9):32-40 (September, 1974). © 1974, American Institute of Physics.
The late Gerard K. O’Neill was professor of physics at Princeton University.
Careful engineering and cost analysis shows we can build pleasant, self-sufficient dwelling places in space within the next two decades, solving many of Earth’s problems.
New ideas are controversial when they challenge orthodoxy, but orthodoxy changes with time, often surprisingly fast. It is orthodox, for example, to believe that Earth is the only practical habitat for Man, and that the human race is close to its ultimate size limits. But I believe we have now reached the point where we can, if we so choose, build new habitats far more comfortable, productive and attractive than is most of Earth.
Although thoughts about migration into space are as old as science fiction, the technical basis for serious calculation did not exist until the late 1960’s. In addition, a mental “hangup” — the fixed idea of planets as colony sites — appears to have trapped nearly everyone who has considered the problem, including, curiously enough, almost all science-fiction writers. In recent months I learned that the space pioneer Konstantin Tsiolkowsky, in his dreams of the future, was one of the first to escape that hangup.
By chance, and initially almost as a joke, I began some calculations on the problem in 1969, at first as an exercise for the most ambitious students in an introductory physics course. As sometimes happens in the hard sciences, what began as a joke had to be taken more seriously when the numbers began to come out right. There followed several years of frustrating attempts to get these studies published.
Friends advised that I take my ideas “to the people” in the form of physics lectures at universities. The positive response (especially from students) encouraged me to dig harder for the answers to questions about meteoroid damage, agricultural productivity, materials sources, economics and other topics. The results of that study indicate that
- we can colonize space, and do so without robbing or harming anyone and without polluting anything.
- if work is begun soon, nearly all our industrial activity could be moved away from Earth’s fragile biosphere within less than a century from now.
- the technical imperatives of this kind of migration of people and industry into space are likely to encourage self-sufficiency, small-scale governmental units, cultural diversity and a high degree of independence.
- the ultimate size limit for the human race on the newly available frontier is at least 20,000 times its present value.
How can colonization take place? It is possible even with existing technology, if done in the most efficient ways. New methods are needed, but none goes beyond the range of present-day knowledge. The challenge is to bring the goal of space colonization into economic feasibility now, and the key is to treat the region beyond Earth not as a void but as a culture medium, rich in matter and energy. To live normally, people need energy, air, water, land and gravity. In space, solar energy is dependable and convenient to use; the Moon and asteroid belt can supply the needed materials, and rotational acceleration can substitute for Earth’s gravity.
Space exploration so far, like Antarctic exploration before it, has consisted of short-term scientific expeditions, wholly dependent for survival on supplies brought from home. If, in contrast, we use the matter and energy available in space to colonize and build, we can achieve great productivity of food and material goods. Then, in a time short enough to be useful, the exponential growth of colonies can reach the point at which the colonies can be of great benefit to the entire human race.
To show that we are technically able to begin such a development now, this discussion will be limited to the technology of the 1970’s, assuming only those structural materials that already exist. Within a development that may span 100 years, this assumption is unrealistically conservative. We shall look at the individual space communities — their structure and appearance and the activities possible for their inhabitants, their relation to the space around them, sources of food, travel between communities as well as to Earth, the economics of the colonies and plans for their growth. As is usual in physics, it is valuable to consider limiting cases; for this study, the limits are an eventual full-size space community on a scale established by the strength of materials, and a first model, for which cost estimates can reasonably be made. The goals of the proposal will be clearer if we first discuss the large community.
A cylindrical habitat
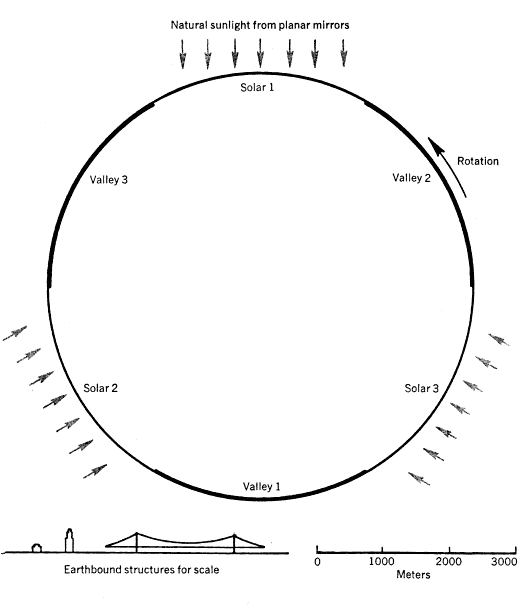
The geometry of each space community is fairly closely defined if all of the following conditions are required: normal gravity, normal day and night cycle, natural sunlight, an earthlike appearence, efficient use of solar power and of materials. The most effective geometry satisfying all of these conditions appears to be a pair of cylinders. The economics of efficient use of materials tends to limit their size to about four miles in diameter, and perhaps about 16 miles in length. (See figure 1.) In these cylinder pairs, the entire land area is devoted to living space, parkland and forest, with lakes, rivers, grass, trees, animals and birds, an environment like most attractive parts of Earth; agriculture is carried on elsewhere. The circumference is divided into alternating strips of land area “valleys”) and window area (“solars”). The rotation period is two minutes, and the cylinder axes are always pointed toward the Sun.
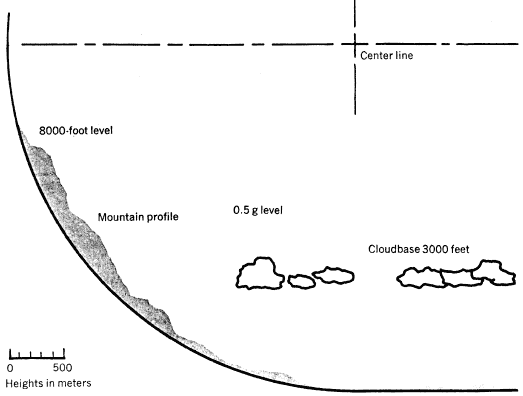
Figure 1. Section of a space-community main cylinder (top). The circumference is divided into alternating strips of land area (valleys) and window area (solars). Although the space-community valleys offer new landscaping opportunities and architectural possibilities, it is reassuring to note that certain Earth features can be recreated: the side view of a cylinder end cap (bottom) includes a mountain profile taken from an aerial photograph of a section of the Grand Teton range in Wyoming.
Because the Moon is a rich source both of titanium and of aluminum, it is likely that these metals will be used extensively in the colonies. For conservatism, though, the calculation of the cylinder structure has been based on the use of steel cables, to form “longerons” (longitudinal members carrying the atmospheric forces on the end caps) and circumferential bands (carrying the atmospheric force and the spin-induced weights of the ground, of the longerons and of themselves). For details of this calculation and the assumptions it includes, see the box [below]. The steel cables are bunched to form a coarse mesh in the window areas. The bands there subtend a visual angle of 2.3 x10-4 radians, about equal to the diffraction limit for the sunlight-adapted human eye, and so are nearly invisible. The windows themselves are of glass or plastic, subdivided into small panels.
Steel structure
For the structure, steel cables are assumed to be formed into longerons (average thickness ΔrL) and circular bands (average thickness ΔrB).
The value of ΔrL required is
ΔrL = Rρo/2T
where R is the cylinder radius, ρo the atmospheric pressure and T the tension. For land density ρL and depth xL, and bands of density ρF, the total equivalent internal pressure pT is
pT = ρo + ρLxLg + ρFrBg + ρFrLg
To solve for pT we note that
ΔrB = pTR/T
so that
pT = (ρo + gρLxL + gρFR/T)/(1-gρFR/T)
For an average soil depth of 150 cm, with an average density of 1.5 gm per cc,
po = gρLxL = 1.23 x 105 newtons/m2
To arrive at a conservative value for T, we note that half a century ago, the working stress for suspension-bridge cables was 70,000 to 80,000 pounds per square inch [ref 1].
At that time, D. B. Steinman [ref 1] argued for the use of stresses over 100,000 psi. If we use 1920’s steels, hardened to bring the yield point to 90% of the ultimate strength, and work at 75% of the yield point, the working stress can be 152,000 psi. If we take T as 150,000 psi and R as 3200 meters, the averaged surface mass density is 7.5 tons per square meter.
In the window (solar) areas, the longerons can be 0.8-meter cables in stacks of four at 14-meter intervals. The bands can be in the same arrangement, but with a 1.5-meter diameter, and the mesh transparency will then be 84%. Considerably larger values of R would result from the extensive use of titanium in the structure, together with a thinner layer of earth.
There is no sharp upper limit on the size of a space-community cylinder; with increasing size, though, a larger fraction of the total mass is in the form of supporting cables. The figure 3200 meters for radius R is somewhat arbitrary. Economy would favor a smaller size; use of high-strength materials, or a strong desire for an even more earthlike environment, would favor a larger. Independent of size, the apparent gravity is earth-normal, and the air composition as well as the atmospheric pressure are those of sea level on Earth. For R equal to 3200 meters, the atmospheric depth is that of an Earth location at 3300 meters above sea level, an altitude where the sky is blue and the climate habitable: At any radius r within the cylinder we have
p = poe–a(R2-r2)
where
a ≡ gpo/2Rpo = (1/2R)(1.2 x10–4/meter)
The length of a day in each community is controlled by opening and closing the main mirrors that rotate with the cylinders. The length of day then sets the average temperature and seasonal variation within the cylinder. Each cylinder can be thought of as a heat sink equivalent to 3 x108 tons of water; for complete heat exchange, the warnup rate in full daylight would be about 0.7 deg C per hour. As on Earth, the true warmup rate is higher because the ground more than a few centimeters below the surface does not follow the diurnal variation.
Bird and animal species that are endangered on Earth by agricultural and industrial chemical residues may find havens for growth in the space colonies, where insecticides are unnecessary, agricultural areas are physically separate from living areas, and industry has unlimited energy for recycling.
As we can see in figure 1, it is possible to recreate certain Earth features: the mountain profile is taken from an arieal photograph of a section of the Grand Teton range in Wyoming. The calculated cloud base heights as seen in the figure are typical of summer weather on Earth: For a dry adiabatic lapse rate of 3.1 deg per 300 meters and a dew-point lapse rate of 0.56 deg per 300 meters, relative humidity and a temperature range between zero and 32°C, the cloud base heights range between 1100 and 1400 meters.
Environmental control
The agricultural areas are separate from the living areas, and each one has the best climate for the particular crop it is to grow. Gravity, atmosphere and insolation are earthlike in most agricultural cylinders, but there is no attempt there to simulate an earthlike appearence. Selected seeds in a sterile, isolated environment initiate growth, so that no insecticides or pesticides are needed. (The evolution time for infectious organism is long, and resterilization of a contaminated agricultural cylinder by heating would not be difficult.) All food can be fresh, because it is grown only 20 miles from the point of use. The agricultural cylinders can be evenly distributed in seasonal phase, so that at any given time several of them are at the right month for harvesting any desired crop.
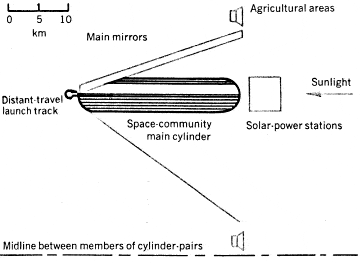
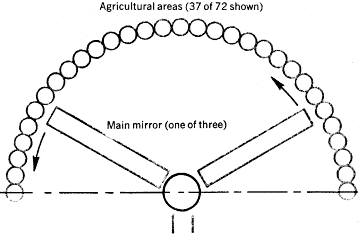
Figure 2 shows side and end views of a space community as a complete ecosystem. The main mirrors are made of aluminum foil and are planar. Moving these mirrors varies the angle at which sunlight hits the valleys (controlling the diurnal cycle), and the Sun appears motionless in the sky, as it does on Earth. The solar power stations, which consist of paraboloidal mirrors, boiler tubes and conventional steam-turbine electric generators, can provide the community with sufficient power, easily up to ten times the power per person now used (10 kw) in highly industrialized regions [ref 2]. For such energy-rich conditions (120 kw per person) the power needed for a cylinder housing 100,000 people is 12,000 megawatts: The solar power incident on a cylinder end cap is 36,000 megawatts, adequate if the thermal efficiency is 33%. Extra power plants near the agricultural ring would be needed for higher population density. Waste heat is sent into space by infrared radiators of low directionality.
Figure 2. Space community as a whole is seen in side (top) and end (bottom) views For the end view, 37 of the 72 agricultural cylinders in a ring are shown; the ring does not rotate as a whole. Note the lines of symmetry in both sections of the figure.
The communities are protected from cosmic rays by the depth of the atmosphere and by the land and steel supporting structure, the bands and longerons being distributed where visual transparency is unnecessary. Meteoroid damage should not be a serious danger. Most meteoroids are of cometary rather than asteroidal origin and are dust conglomerates, possibly bound by frozen gases [ref 3]; a typical meteoroid is more like a snowball than like a rock. Spacecraft sensors have collected abundant and consistent data on meteoroids in the range 10-6 to 1 gram, and the Apollo lunar seismic network is believed to have 100% detection efficiency for meteoroids [ref 4] above 10 kg: Data from these sources are consistent with a single distribution law.
The Prairie Network sky-camera data [ref 5], after substantial correction for assumed luminous efficiency, agree with data from the National Aeronautics and Space Administration for 10-gm meteoroids. The spacecraft and seismic data indicate a mean interval of about one-million years for a strike by a heavy (one ton) meteoroid on a space community of cross section 1000 square kilometers. Even such a strike should produce only local damage if the structure is well designed. For 100-gram meteoroids, the mean interval for a strike is about three years. From the combined viewpoints of frequency and of momentum carried, the size range from one to ten grams may need the most care in window design and repair methods. For total breakage of one window panel, Daniel Villani at Princeton has calculated a leakdown time of about 300 years. Meteoroid-damage control is, then, a matter of sensing and of regular minor repair rather than of sudden emergencies.
Axial rotation and transport
A key element in the design of the space colony is the coupling of two cylinders by a tension cable and a compression tower to form a system that has zero axial angular momentum and is therefore able to maintain its axis pointed toward the Sun without the use of thrusters. The force and torque diagram for this arrangement is seen in figure 3. To accelerate the cylinders up to the required rotational speed, static torque is transmitted through the compression framework that joins the two cylinders of a pair. For a spin-up time of three years, a constant 560,000 horsepower is needed; this is 3% of the generator capacity of a cylinder. After spinup, the same motors can provide maintenance power for frictional losses and for attitude control about the spin axis. Each cylinder’s angular momentum is 1.5 x1018 kg2 rad per sec; the torque needed to precess this angular momentum once each year is 3 x1011 newton meters, corresponding to a constant force of 1200 tons on a 26-km lever arm.
Figure 3. Force and torque diagram for a cylinder. Nondissipative static forces are used to precess spin angular momenta, so that cylinder axes always point toward the Sun.
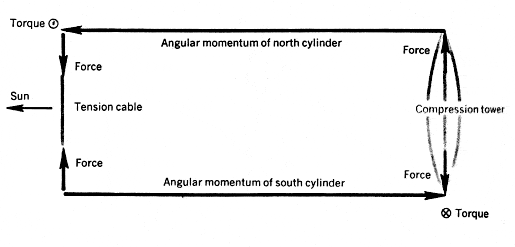
The phase difference of seasons between the two cylinders permits “seasonal counterpoint,” midsummer in one cylinder during midwinter in the other. Travel between the two requires no power and only nine minutes of time. They are only 90 km apart, and engineless vehicles can unlock from the outer surface of one cylinder at a preset time, move in free flight with the tangential velocity (180 meters per sec or 400 miles per hour) and lock on to the other cylinder at zero relative velocity.
Travel between communities can also be carried out with simple engineless vehicles, accelerated in a computed direction by a stationary cable-pulling electric motor and decelerated by an arresting cable at the destination. The “cable-car” vehicles for such free flight need no fuel, no complex maintenance nor a highly trained crew, and should be inexpensive. Vehicle speeds permit travel among a total population larger than that of Earth within flight times of seven hours. (I have here assumed communities spaced at 200-km intervals, so that the maximum dimension of a planar cluster housing 4 billion people is 29,000 km. For a vehicle with acceleration 1g and the required travel time of seven hours, the acceleration length is 66 km.) With no need for aerodynamic design, the vehicles can be far more roomy and comfortable than the typical earthbound commercial jet.
Life in the colonies
The key statements so far have been based on known facts, on calculations that can be checked and on technology whose costs can be estimated realistically. The discussion, however, would be sterile without some speculations that must, of course, be consistent with the known facts.
With an abundance of food and clean electrical energy, controlled climates and temperate weather, living conditions in the colonies should be much more pleasant than in most places on Earth. For the 20-mile distances of the cylinder interiors, bicycles and lowspeed electric vehicles are adequate. Fuel-burning cars, powered aircraft and combustion heating are not needed; therefore, no smog. For external travel, the simplicity of engineless, pilotless vehicles probably means that individuals and families will be easily able to afford private space vehicles for low-cost travel to far distant communities with diverse cultures and languages. The “recreational vehicles” of the colonial age are therefore likely to be simple spacecraft, consisting of well furnished pressure shells with little complexity beyond an oxygen supply and with much the same arrangement of kitchen facilities and living space as are found today in our travelling homes.
All Earth sports, as well as new ones, are possible in the communities. Skiing, sailing, mountain climbing (with the gravity decreasing linearly as the altitude increases) and soaring are examples. As an enthusiastic glider pilot, I have checked the question of thermal scales: The soaring pilots of the colonial age should find sufficient atmospheric instability to provide them with lift. At high altitudes, man-powered flight — a nearly impossible dream on Earth — becomes easy. A special, slowly rotating agricultural cylinder with water and fish can have gravity 10-2 or 10-3 times that on Earth for skin diving free of pressure-equalization problems. Noisy or polluting sports, such as auto racing, can easily be carried out in one of the cylinders of the external ring.
The self-sufficiency of space communities probably has a strong effect on government. A community of 200,000 people, eager to preserve its own culture and language, can even choose to remain largely isolated. Free, diverse social experimentation could thrive in such a protected, self-sufficient environment.
If we drop our limitation to present technology, the size of a community could be larger. One foreseeable development is the use of near-frictionless (for example, magnetic) bearings between a rotating cylinder and its supporting structure, which need not be spun. For eight tons per square meter of surface density and a tensile strength of 300,000 psi, R would be 16 km, the total area would 50,000 km2, and the population would be between five million (low density) and 700 million (the ecological limit, the maximum population that can be supported).
In Table 1 we see my estimate of the earliest possible schedule for space colonization, beginning with a model community in the late 1980’s. From about the year 2014, I assume a doubling time of six years for the colonies; that is, the workforce of a “parent” colony could build a “daughter” colony within that time. In making these estimates I have calculated that the first model community would require a construction effort of 42 tons per man-year, comparable to the effort for large-scale bridge building on Earth. Full-size communities at high population density require 50 tons per man-year, and up to 5000 tons per man-year for low population density. For comparison, automated mining and shipping in Australia now reaches 200 tons per man-year averaged over a town [ref 6].
Table 1: Possible Stages in the Development of Space Communities
Model | Length (km) | Radius (m) | Period (sec) | Population* | Earliest estimated date |
1 | 1 | 100 | 21 | 10,000 | 1988 |
2 | 3.2 | 320 | 36 | 100-200 x 103 | 1996 |
3 | 10 | 1000 | 63 | 0.2-2 x 106 | 2002 |
4 | 32 | 3200 | 114 | 0.2 – 20 x 106 | 2008 |
*Population figures are for double unit; higher figures are the approximate ecological limits, for conventional agriculture.
In the long run, space-colony construction is ideally suited to automation. A colony’s structure consists mainly of cables, fittings and window panels of standard modular form in a pattern repeated thousands of times. The assembly takes place in a zerogravity environment free of the vagaries of weather. By the time that the colonies are evolving to low population density, therefore, I suspect that very few people will be involved in their construction. Most of the workforce will probably be occupied in architecture, landscaping, forestry, zoological planning, botany and other activities that are nonrepetitive and require a sense of art and beauty.
Our new options
It is important to realize the enormous power of the space-colonization technique. If we begin to use it soon enough, and if we employ it wisely, at least five of the most serious problems now facing the world can be solved without recourse to repression: bringing every human being up to a living standard now enjoyed only by the most fortunate; protecting the biosphere from damage caused by transportation and industrial pollution; finding high-quality living space for a world population that is doubling every 35 years; finding clean, practical energy sources; preventing overload of Earth’s heat balance.
I hesitate somewhat to claim for space-colonization the ability to solve one other problem, one of the most agonizing of all: the pain and destruction caused by territorial wars. Cynics are sure that humanity will always choose savagery even when territorial pressures are much reduced. Certainly the maniacal wars of conquest have not been basically territorial. Yet I am more hopeful; I believe we have begun to learn a little bit in the past few decades. The history of the past 30 years suggests that warfare in the nuclear age is strongly, although not wholly, motivated by territorial conflicts; battles over limited, nonextendable pieces of land.
From the viewpoint of international arms control, two reasons for hope come to mind. We already have an international treaty banning nuclear weapons from space, and the colonies can obtain all the energy they could ever need from clean solar power, so the temptations presented by nuclear-reactor byproducts need not exist in the space communities.
To illustrate the power of space-colonization in a specific, calculable situation, we trace the evolution of a worst-case example: Suppose the present population-increase rate were to continue on Earth and in the space colonies. In that case the total human population would increase 20,000-fold in a little over 500 years. Space-colonization would absorb even so huge a growth, as we shall see from our calculations.
The total volume of material needed in a full-size community is 1.4 x109 cubic meters, and the material available in the asteroid belt (from which the later communities will be built) is estimated to be 4 x1017 cubic meters, about one twenty-five hundredth the volume of Earth. For a present world population of 3.9 x 109 people and a growth rate [ref 7] of 1.98% per year (the 1965-71 average), the asteroidal material would last 500 years, corresponding to a 20,000-fold population increase at low population density.
In figure 4, we see the development of this worst-case problem. To hasten the solution of that problem, the initial space community population density is taken as the ecological limit; the maximum number of people that can be supported with food grown within the communities, with conventional agriculture. Richard Bradfield has grown enough to feed 72 people per hectare by the techniques of double planting and multiple cropping, and with the use of cuttings for livestock feed. These results [ref 8], as published and also as described to me by Bradfield, were obtained in the Phillipines, which has only a nine-month growing season and less than ideal weather conditions. Calculations based on his figures, but assuming an ideal twelve-month season, indicate that the colonies should be able to support 143 people per hectare with a diet of 3000 calories, 52 grams of usable protein and 4.3 pounds of total food per person per day [ref 9]. Much of the protein would come from poultry and pork. The two main cylinders of Model 1 should then be able to support up to 10,800 people, and the corresponding ecological limit for a full-size community would be 20 million people. At this limit, all the colonists would have a high standard of living, but in apartment-house living conditions, looking out over farmland. For a community limit of 13-million people, the main cylinders could be kept free of agriculture.
Figure 4. Effectiveness of space colonization in solving a hypothetical “worst case” population-growth problem. The case considered assumes no reduction of population growth rate either on Earth or in the space colonies. Here PE is the population of Earth, PS that of space, and AS/AE the ratio of land area in space (all usable) to total land area of Earth. Both PE and PS/AS reach stable, relatively low values. Changes within wide limits in the assumed input numbers do not affect the reaching of a stable solution, nor do they affect the final stable values of PE and PS/AS. This figure is an example of the power of space-colonization, not a prediction.
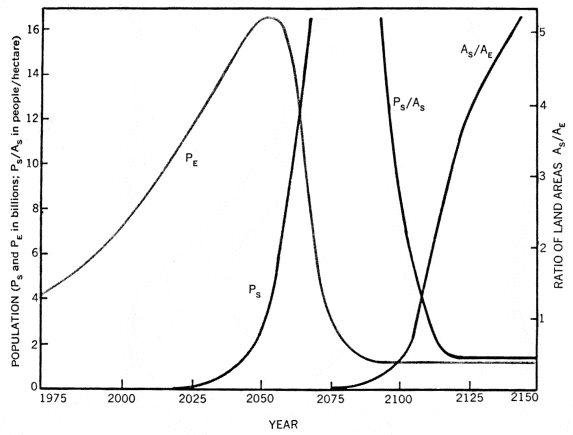
By about 2050, then, figure 4 indicates that emigration to the colonies could reverse the rise in Earth’s population, and that the acceleration of the solution could be dramatically fast: Within less than 30 years, Earth’s population could be reduced from a peak of 16.5 billion people to whatever stable value is desired. I have suggested 1.2 billion as a possible optimum; it corresponds to the year 1910 in Earth history. The reduction in population density in the space communities could be equally rapid, and within another 40 years new construction could thin out the communities to a stable density of 1.43 people per hectare, about one hundredth of the ecological limit. The total land area in the colonies would then be more than three times that of Earth.
We can hope that, in contrast to this worst-case example, some progress toward zero population growth [ref 10] will be made in the next 75 years. Any such progress will hasten the solution, reduce Earth’s population peak, and hasten the day when the population densities on Earth as well as in the colonies can be reduced to an optimum value.
Building the first colony
A responsible proposal to begin the construction of the first colony must be based on a demonstration, in some detail, of one workable plan with realistic cost estimates. I emphasize two points about any such plan: The details presented should be thought of simply as an existence proof of feasibility; and many variations are possible. The optimum design and course of action can only be decided on after study and consultation among experts in a number of fields.
The nominal values for the first model colony are taken as: construction force, 2000 people; population, 10,000; total mass, 500,000 tons. When the design and cost analysis are done in detail for the entire enterprise, the need to fit a budget may force some reduction in size. The initial estimates have been aimed at holding the cost equal to that of one project we have already carried through: Apollo. The choice of 10,000 as a target population ensures that, even with some reduction, Model 1 will be large enough to obtain economies of scale and to serve as an effective industrial base for the construction of Model 2. A much reduced colonization project would be little more than a renamed space station, perhaps able to maintain itself but incapable of building the larger models that are necessary if the program is ultimately to support itself. It is an essential feature of the colonization project that Earth should no longer have to support it after the first two or three stages.
Ultimately, colonization could take place in the entire sphere, 3 x 1017 km2 in area, that surrounds the Sun at the distance we have evolved to prefer (the so-called “Dyson sphere”). For the first colony it is probably best to choose a particular point on that sphere, within easy range of both Earth and Moon, not so close as to be eclipsed often, and preferably stable against displacements in all three coordinates. The L4 and L5 Lagrange libration points satisfy all these conditions. They have the further advantage of forming only a very shallow effective-potential well [ref 11].
Earth, Moon, Sun and the colony form a restricted four-body gravitational problem, for which the full solution has only been worked out within the past several years [ref 12]. The stable motion is a quasielliptical orbit, of large dimensions, about L5. The maximum excursions in arc and radius are several tenths of the Earth-Moon distance. On the stable orbit there is room for several thousand colonies; a long time will pass before colonization can fill so big an orbit.
Cost minimization
There are several key problems involved here, each of which appears to yield to an efficient solution in principle: reducing freight-shipment cost from the Earth to L5, the colony site; minimizing the mass needed from Earth; designing a device for low-cost transfer of materials from the Moon to L5.
The first problem was considered by Robert Wilson (NASA), Eric Hannah and George Hazelrigg (Princeton) at a meeting held 9 and 10 May at Princeton (A Proceedings of this meeting will be published). Their conclusion was that the best method during the 1980’s will probably be conventional chemical rockets — specifically, the high-quality engines already being developed for the space shuttle. Among several variations possible, the common feature was reusability, and the cost estimates for shipment varied from $190 to $400 per pound, in 1972 dollars. The cost summary table (Table 4) therefore assumes $425 per pound.
To reduce the mass needed from Earth, most of the repetitive structural members (aluminum) and window panels (glass) must be produced at L5 from lunar material. A further, important saving is made by getting 89% of the mass of needed water from oxygen in the plentiful lunar-surface oxides, bringing only 11% of the water mass as liquid hydrogen from Earth. Of the 500,000-ton total mass (see Table 2) for the Model 1 colony, 98% can be obtained from the Moon. The elements most needjed are aluminum, titanium, silicon and oxygen. Lunar surface soil is usable for agriculture, with the addition of nitrates and small amounts of trace elements. The remaining 10000 tons must come from the Earth.
Table 2. Masses of Materials Required for Model 1 (Metric tons)
Total mass required | Mass required from Earth | |
| Aluminum (container, structures) | 20,000 | – |
| Glass (solars) | 10,000 | – |
| Water | 50,000* | – |
| Generator plant | 1000** | 1000 |
| Initial structures | 1000 | 1000 |
| Special fabricated hardware | 1000 | 1000 |
| Machines and tools | 800 | 800 |
| Soil, rock and construction materials | 420,000* | – |
| Liquid hydrogen | 5400 | 5400 |
| 2000 people and equipment | 200 | 200 |
| Dehydrated food | 600 | 600 |
| Totals | > 500,000 | 10,000 |
*Includes replenishable reserves to be used to initiate construction of Model 2, and so are higher than the minima required for Model 1.
**For 100 MW plant.
To bring the total cost within practical limits, we must develop a low-cost method for transporting raw materials from the Moon to the construction site. The discussion of transport methods should be taken as an existence proof rather than as a detailed design. There may very well be better methods than those I have considered; however, it is enough to show two solutions that appear to be workable. Both use the two great advantages of the lunar environment: an excellent vacuum and a very low escape velocity, about 1.5 miles per sec, less than one quarter of the escape velocity from Earth. To bring a kilogram to L5 from the Moon takes less than 5% of the energy needed to take a kilogram from Earth.
Both methods assume electric power from a conventional steam-electric power plant that uses solar energy, and both assume that the system runs only during the lunar day, the night being used for scheduled maintenance, crew rest and possibly materials processing. I have also assumed another factor of two lost to system breakdowns. Overall then, each system is assumed to be running only one week in four.
The first method, called “RPL” for rotary pellet launcher, is a symmetric, two-arm propeller-like device, running at constant speed. (See box [below] for description). To transfer 500 tons in six years, about 26 such RPL’s would be needed, for a total power of 32 MW. Precise steering is carried out by a linear electromagnetic deflection-plate system after the launching, to hold down the pellet dispersion and permit easy collection.
Rotary pellet launcher
The rotary launcher is assumed to be a symmetric two-arm propeller-like device, running at constant speed, with launching arms of ten-meter radius.
Mass: 10 tons
Rotation rate: 2300rpm
Tip speed: 2400 m/sec (escape velocity)
Power: 1600 horsepower
The transfer rate per launcher is 3250 tons per year for the transfer of 5-gm pellets, assuming a 25% duty cycle. The strength-to-mass ratio for the launcher is within the range attainable by boron-filament technology: An aluminum matrix containing boron grown on tungsten cores is calculated to have a yield stress of 322,000 psi and average density 4.1, so that
ρ/T = 1.85 x 10-6
Here ρ is the density and T the tension in MKS units. For uniform stress, the ratio of arm radii at the base and the tip r1 and r2) is
log r1/r2 = (ρ / 4T)v2
where v is the escape velocity. For r1/r2 less than 50, ρ/T must be less than 2.08 x 10-6.
The alternative method, called “TLA” for transport linear accelerator, uses the technology of dynamic magnetic levitation and the linear synchronous motor. The TLA is a recirculating system of small, passive vehicles (buckets), each having no moving parts but containing superconducting coils. The bucket accelerates a 9-kg payload to escape speed along a magnetic-levitation, linear-synchronous track. Deceleration then releases the payload, the bucket slows to a moderate speed, and is recirculated to receive another payload. Table 3 shows some guideline parameters. The mass estimate is 1500 tons, of which about 80% is in power-generation and power-handling equipment. In six years, running 25% of the time, the TLA can transport over 300 times its own weight. (For a short bibliography of early work on the possibilities of electromagnetic launching, before the development of dynamic magnetic levitation, see reference 13.)
| Table 3. Guideline Parameters for Transport Linear Accelerator |
|
| *LSM: linear synchronous motor |
Both RPL and TLA may have eventual applications as high-throughput energetically efficient reaction motors running on solar power and able to use any kind of asteroidal debris as reaction mass. They could propel very large payloads in the million-ton range or higher, between the asteroid belt and the L5 site.
The Model 1 colony will be too small to carry out a wide variety of manufacturing processes, but it can perform those tasks that are energy intensive, not labor intensive, and that will produce a large return in total tonnage. One example is the production of aluminum by the Hall process. An installed capacity of 40 MW is enough to produce 20,000 tons of aluminum in two years, for the exostructure of Model 1. Another example is the separation of oxygen from the lunar oxides to combine with hydrogen brought from Earth. (With 50,000 tons of water, Model 1 can have lush vegetation as well as substantial streams and small lakes). In contrast, small, low-mass parts are best brought from Earth.
The later colonies, perhaps beginning with Model 3, will use asteroidal material, which is rich in hydrocarbons as well as in metals. We can speculate that, relatively early in the development of the colonies, the economics of freight transport will probably dictate that the “up” shipments from Earth will consist only of people and labor-intensive, miniaturized products such as computers and calculators. The “down” shipping costs may be lower because of the possibility of atmospheric braking. Between colonies, all shipping and travel costs should be very low. For Model 1, the project cost is summarized in Table 4. For comparison, the Apollo project cost about 33 billion (1972) dollars.
Table 4. Estimated Cost of Building Space Colonies (in 1972 dollars)
Model 1 | Model 2 | |||
Item | Unit cost | Total (in $109) | Unit cost | Total (in $109) |
| Launch vehicles | 0.3 x 109 | 0.9 | 0.5 x 105 | 1.5 |
| Transport E→L5 | 425/lb | 8.5 | 250/lb | 11.0 |
| People E→L5 | 1000/lb | 2.2 | 500/lb | 8.8 |
| Transport E→M | 1000/lb | 6.6 | 500/lb | 2.2 |
| Equipment for Moon | 400/lb | 2.4 | 400/lb | 1.8 |
| Equipment for L5 | 180/lb | 1.2 | 400/lb | 2.0 |
| Machines and tools (L5) | 625/lb | 1.1 | 625/lb | 2.8 |
| Salaries (L5) | 50,000 man-year | 0.6 | (25% on Earth) | 2.0 |
| Salaries (Earth) | 30,000 man-year | 7.2 | (30,000 man-year) | 2.0 |
| Totals | 30.7 | 34.1* | ||
($5.1 x 109/yr) | (4.3 x 109/yr)* | |||
*The cost saving due to the presence of Model 1 can be divided as follows: production, 25,000 lbs/man-year; workforce, 4000 people; transport costs, $250/lb. The saving over the eight years needed to complete the colony is thus a total of $200 x 109.
We can also see in Table 4 that the economic payoff from the construction of the first community will come quickly, during construction of the second. That payoff will be in the form of transport costs saved because tools and fabricated structures will be made from lunar material at Community 1 rather than on Earth. The first colony can apparently pay for itself in one or two years, and, by its presence, can keep the annual cost of building Community 2 — with its 100,000 to 200,000 people — at about the same level as for Community 1. After that, construction costs for models 3, 4 and so on, should taper off as space-based industry becomes stronger, and as the wide range of chemical elements in the asteroids are used.
We can speculate that the second or third colony may begin to pay back its construction cost in additional ways, for example by the manufacture of high-strength single crystals [ref 14] in the zerogravity, high-vacuum environment that surrounds it, and by the manufacture of titanium products.
To follow the economics as far as Model 3 would be too speculative; its costs to Earth will mainly be those of transporting its one to two million inhabitants to L5. Its earliest possible completion date is estimated at just after the turn of the century (28 years forward in time; going back the same number of years brings us to the era of the V2 rocket, more than ten years before the first artificial satellite). Around the year 2000, a fully reusable chemical rocket system could transport payloads to L5 at a cost of about $100 per pound (again, in 1972 dollars). A prospective colonist could therefore save enough money (one or two years’ salary) to emigrate with his family of three. The near certainty of continued advances in propulsion systems suggests that the actual costs will be lower.
By the middle years of the next century, and possibly earlier, production costs at L5 should be lower than on Earth. My reasons for this belief are that:
- the asteroid belt is a rich source of raw materials, already exposed and differentiated.
- transport from the belt to L5 can be done in a way analogous to ocean freight on Earth; that is, in very large units, with low fuel costs and very small crews. In space, it may be most practical to eliminate the freighter hulls entirely. A TLA-type reaction motor can run on free solar power and transport an entire asteroid to L5, perhaps with no crew at all.
- food-raising costs, production costs and shipping costs among the communities should all be lower than on Earth because of ideal growing conditions, proximity of farms to consumers, availability of unlimited solar power and the convenience of zero-gravity and high-vacuum environments for production and transportation.
If we are so prodigal as to run through the entire material of the asteroid belt in the next 500 years, we can even gain another 500 years by using up the moons of the outer planets. Long before then, I hope we will have slowed the growth of the human population. And I feel sure that long before then a modified version of a space community will have travelled to a nearby star.
I am left with the desire to communicate two aspects of this work more completely. On the one hand, I would like to display for review more of the details of calculations and references than is possible here. And on the other hand, I am acutely aware of the need for discussion outside our own group of physics-oriented people. This work should be discussed and debated as widely as possible, by people with a range of technical and artistic talents, and by people who claim no special talent beyond the ability to work hard for a worthwhile goal. I hope I have conveyed at least a little of the sense of excitement that I have enjoyed over the past few years as each serious problem has appeared to yield to a solution, as well as how much more remains to be done and how much need there is for good ideas and hard work.
For private communications leading to references, I thank Donald Gault, Barry Royce, Richard Johnson, George Hazelrigg and John Breakwell. And it is a special pleasure to thank those who encouraged me to continue this work in the years when it was little known, particularly George Pimentel, Freeman Dyson, Brian O’Leary, Roman Smoluchowski, Richard Feynman and John Tukey. I am also grateful to Michael Phillips of the Point Foundation, which supported the first public meeting on this subject.
References
- G. A. Hool, W. S. Kinne, Movable and Long Span Steel Bridges, McGraw-Hill, New York, (1943), page 328; D. B. Steinman, A Practical Treatise on Suspension Bridges, John Wiley, New York (1929), page 236.
- S. F. Singer, Scientific American, September 1970, page 174.
- “Meteoroid Environment Model — 1969 (Near Earth to Lunar Surface),” NASA SP-8013.
- G. Latham, J. Dorman, F. Duennebier, M. Ewing, D. Lammlein, Y. Nakamura, “Moonquakes, Meteorites and the State of the Lunar Interior,” and “Lunar Seismology,” in Abstracts of the Fourth Lunar Science Conference, 1973, Lunar Science Institute, 3303 NASA Road 1, Houston, Texas 77058.
- R. E. McCrosky, “Distributions of Large Meteoric Bodies,” Smithsonian Astrophysical Observatory Special Report No. 280.
- K. MacLeish, “Australia’s Wild,” in National Geographic 143, no. 2, 168, (1973).
- “1970 World Population Data Sheet,” Population Reference Bureau Inc, 1755 Massachusetts Ave, N. W., Washington, D.C. 20036.
- R. Bradfield, “Multiple Cropping-Hope for Hungry Asia,” in Reader’s Digest, October 1972, page 217.
- F. M. Lappe, Diet for a Small Planet, Ballantine Books, New York, (1971).
- “The Limits of Development,” Report by the Systems Dynamics Group, Massachusetts Institute of Technology (1972), Club of Rome, Geneva.
- W. H. Michael Jr, “Considerations of the Motion of a Small Body in the Vicinity of the Stable Libration Points of the Earth-Moon System,” NASA TR-R-160 (1963).
- R. Kolenkiewicz, L. Carpenter, “Stable Periodic Orbits About the Sun-Perturbed Earth-Moon Triangular Points,” AIAA Journal 6, no. 7, 1301 (1968); A. A. Kamel, “Perturbation Theory Based an Lie Transforms and its Application to the Stability of Motion Near Sun-Perturbed Earth-Moon Triangular Libration Points,” NASA CR-1622, August 1970.
- A. C. Clarke, J. Brit. Interplanetary Soc. 9, 261(1950).
- H. C. Gatos, A. F. Witt, “Crystal Growth Studies on Skylab,” MIT News Release 14 May 1974.






