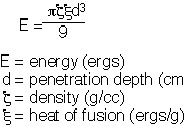 (1)
(1)The risk of damage by collision with meteoroids can be assessed if the flux of meteoroids as a function of mass values can be determined. Data to do this come from three sources:
In the meteoroid mass range from 10^-6 to 1 g spacecraft sensors provide abundant data, and for masses above 10 kg the lunar seismic network is believed to be 100 percent efficient in assessing the flux.
Earth based data are subject to large corrections but agree with space data at the 1 0-g value.
Figure 2-5 shows the distribution law (integral flux) for meteoroid masses of interest to the problem of habitat protection. The Prairie Network data are not shown because they are subject to large corrections of an uncertain nature. The type of meteoroid structure most commonly found in space is a conglomerate of dust bound together by frozen gases. This has been described as a "dirty snowball" as opposed to a stoney or nickel-iron rock that remains at the Earth's surface after a meteorite survives passage through the atmosphere. The hazard of meteors is not necessarily that of a single collision. Because meteors occasionally occur in clusters or "showers," they could, by a series of hits, initiate a chain of failures otherwise impossible. On an average night an observer will see about 10 meteors an hour. During the most intense of annual showers the observation rate rises to about 50 an hour. Thus the existence of annual showers causes temporary flux enhancements by perhaps a factor of 5. In the year 1833 the hourly rate over Paris from the shower of Leonids rose to 35,000 an hour - an increase in flux of many thousand times. Thus the meteoroid flux can at times increase enormously to constitute a qualitatively different kind of hazard from the usual situation. A detailed analysis of what risk such a shower would entail must await a final system model for space habitation and extensive computer simulation. Even so it is apparent that the risk from showers would only occur on a time scale of hundreds of years.
The second piece of knowledge needed to assess meteoroid risk to space habitation is the damage caused by a meteoroid of a given size. There are three mechanisms of destruction. First, a mass traveling at the typical meteoroid velocity of 40 km/s will create a crater in any material object with which it collides. McKinley (ref. 22) quotes Whipple to the effect that the depth of penetration is related to the incident energy by:
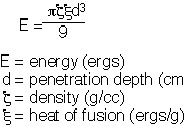 (1)
(1)Whipple is also quoted as saying that a thin metal sheet a meter or so away from the main hull acts as a "meteor bumper" by vaporizing any incident meteoroid and thus minimizing blast loading on the hull through I/r^2 attenuation of the blast wave.
The second damage effect is shock wave destruction of interior structures if a meteoroid penetrates the main hull. Such an event is equivalent to creating an explosion at the point of entry with 200 g of TNT for every gram of meteoroid traveling at 40 km/s. The overpressure in Pa of a strong explosion shock wave is given roughly by
 (2)
(2)As a point of reference, as little as 5 psi (34.5 kPa) overpressure suffices to knock down buildings and kill an average human being.
The third effect of meteoroid impact is the loss of internal atmosphere through the hole created. The repairing of such a hole is not a difficult problem since air flows, though supersonic in the hole region, fall to gentle values a few hole diameters away. The main operational problem for a habitat is efficient detection and repair of any small holes that occur.
Table 2-1 presents the risk factors for a space habitat due to meteoroid impacts. In this table R(2atm) is the radius at which any shock wave created has two atmospheres of overpressure(2) - a high value for a "kill radius!"
Obviously the hazards of meteoroids pose little danger to kilometer-sized habitats.
TABLE 2-1. (gif format)
| Mass of meteoroid,g |
Occurrence/km^2, | Energy J |
Diameter of crater, m |
R(2 atm), m |
Damage (depends on habitat volume) |
|---|---|---|---|---|---|
| 1 | 10 | 8.5 X 10^5 | 0.02 | 2.3 | Loss of window panel, 1%/hr leakdown |
| 100 | 2000 | 8.5 X 10^7 | .09 | 11 | 10-hr leakdown to 40% of one atmosphere |
| 1 X 10^6 | 1 X10^8 | 8.5 X 10^11 | 2 | 230 | Major structural damage |
|
Curator: Al Globus If you find any errors on this page contact Al Globus. |
 |
This site was hosted by the NASA Ames Research Center from 1994-2018 and is now hosted by:
